第六章 数字签名

急急急 期末预习急急急

数字签名基本概念

数字签名概念

• 使用 公钥 加密技术实现，用于 鉴别数字信息与签名者身份 的方法

• 以 电子方式 存储签名信息，在 数字文档 上身份验证。 接收者和第三方能够 验证 文档 来自 签名者，并且文档签名后 没有被修改，

签名者也 不能否认 对文档的签名

数字签名必须保障：

（1） 接收者能够 核实 发送者对文档的签名

（2） 发送者事后 不能否认 对文档的签名

（3） 不能伪造 对文档的签名

数字签名载体

• 一个签名有 消息 和 载体 两个部分，即签名所表示的 意义 和签名的 物理表现形式

传统签名 VS 数字签名

• 传统签名中，签名与文件是一个 物理整体
  • 具有 共同 的载体
  • 物理上的 不可分割 不可复制 的特性
  • 签名与文件的 不可分割 和 不能重复 使用
• 数字签名中，签名与文件是电子形式
  • 没有固定的物理载体 即签名与文件的物理形式和消息已经分开
  • 电子载体是可以 任意分割 复制 的
• 传统签名的验证是通过 与存档手迹对照来确定真伪的 是 主观的、模糊的、容易伪造的 ，从而也是 不安全的
• 数字签名则使用 密码 ，通过 公开算法可以检验的 ，是客观的、精确的、在计算上的是安全的

传统签名基本特点：

• 能与被签文件在物理上 不可分割
• 签名者 不能否认 自己的签名
• 签名 能被伪造
• 容易 被验证

数字签名是传统签名的数字化，要求：

• 能与所签文件 绑定
• 签名者 不能否认 自己的签名
• 签名 不能被伪造
• 容易 被自动 验证

数字签名应具有的特性

（1） 签名是可信的：任何人可验证前面的有效性

（2） 签名是不可伪造的：除合法签名者外，其他人伪造签名是困难的

（3） 签名是不可复制的： 一消息的签名不能复制为另一消息的签名

（4） 签名的消息是不可改变的：经签名的消息不能被篡改

（5） 签名是不可抵赖的： 签名者事后不能否认自己的签名

数字签名： 对身份认证，保持数据完整性，不可否认性

MAC： 可对身份认证，保持数据完整性，但不具有不可否认性

数字签名的构成

数字签名方案的构成

一个数字签名方案包括如下三个算法：

• 密钥生成：产生用户的公私钥
• 签名算法：产生消息的签名
• 验证算法：验收消息的签名是否合法

数字签名的需求

需满足条件

• 必须相对容易生成该数字签名
• 必须相对容易识别和验证该数字签名
• 伪造 该数字签名在 计算上不可行 ，既包括对一个已有的数字签名构造新的消息，也包括对一个消息伪造一个数字签名

RSA签名算法

RSA签名体制

• 体制参数
  • 选两个保密的大素数 p 和 q，计算 $n = p*q$ , $\varphi(n) = (p-1)\cdot(q-1)$；
  • 选一整数e，满足 $ 1<e<\varphi(n)$,且 $gcd(\varphi(n),e) = 1$
  • 计算 d，满足 $d \cdot e \equiv 1 \bmod \varphi(n)$;
  • 以 $\lbrace e,n \rbrace$ 为公钥，$\lbrace d,n \rbrace$ 为私钥

RSA公钥加密体制原理

• 密钥生成

  • 选择两个大素数 p 和 q
  • 计算 $ n = p \cdot q , \varphi = (p-1) \cdot (q-1)$
  • 随机选取e，要求$ e < n $，e 与 $ \varphi $ 没有公因数，即 e 与 $ \varphi $ 互质
  • 选取 d 使得 $ ed \equiv 1 \bmod \varphi(n) $
  • 公钥是 $ (n,e) $，私钥是 $ (n,d) $

• 签名

  设消息为 $ m \in Z_n $，对其签名为 $$ S \equiv m^d \bmod n $$

  S 即为签名

• 验证

  接收方在收到消息 m 和签名 s 后，验证 $$ m \equiv s^e \bmod n $$ 是否成立，若成立，则发送方的签名有效

• 安全性： 大数分解的困难性

  • 如果RSA的模数 n 被成功分解为 $p*q$，则立即获得 $\varphi(n) = (p-1) \cdot (q-1) $
  • 从而能够确定 e 模 $ \varphi(n) $ 的乘法逆元 d ，
  • 因此攻击成功

• 正确性：

  • 因为 $ d \cdot e \equiv 1 \bmod \varphi (n) $
  • 所以 $ s^e \equiv m^{d \cdot e} \equiv m^{1 + k \cdot \varphi (n)} \equiv m^1 \cdot m^{k \cdot \varphi (n)} \equiv m \bmod n $
  • 其中 k 为某个整数

缺点

$$ m \equiv S^e \bmod n $$

（1） 对任意消息 $ y \in Z_n $ ,任何人可以计算 $ x \equiv y^e \bmod n $,因此任何人可以伪造对随机消息 x 的签名

（2） 如果消息 $x_1$ 和 $x_2$ 的签名分别是 $y_1$ 和 $ y_2$ ，则知道 $x_1,x_2,y_1,y_2$的人可以伪造消息 $x_1 \cdot x_2$的签名$y_1 \cdot y_2 $的签名

（3） 在RSA签名方案中，需签名的消息 $ x \in Z_n $，所以每次只能对 $ \lfloor \log_2n \rfloor $位长消息签名，签名速度慢

克服缺陷的方法：签名之前先求消息的Hash值

EIGamal 签名算法

• 1985年 EIGamal 提出了一个基于离散对数问题的签名方案，后来称为 EIGamal 数字签名方案
• 1991年该数字签名方案的变形被美国国家标准局（NIST）确定位数字签名标准（DSS）

EIGamal签名体制

• 体制参数
  • p：大素数
  • g：$Z^*_p $的一个生成元
  • x：用户A的密钥，$x \in Z^*_p$
  • y：用户A的公钥，$y \equiv g^x(\bmod p)$
  • K: 随机数，用于计算 $r = g^k \bmod p$, $r$ 是签名之一
• 参数要求：
  • P 应为150位以上的十进制数，500位以上的二进制数，p-1 应有大素数因子
  • K 必须是保密而且必须是一次性的
    • K 泄露，则敌手可以计算 $ y^K $从而可以计算出 M
    • 使用同一 K 加密不同的明文 M ，M’ ，如果敌手知道 M 就可以由 $ C_2 / C_2^{‘} = M / M^{‘}$求出M‘

EIGamal公钥加密体制原理

• 密钥生成

  • 选取大素数 p ，$g \in Z^*_n $ 是一个生成元， p 和 g 公开
  • 随机选整数 $ x, 1 \leq x \leq p-2 $,计算 $ y = g^x \bmod p $
  • 公钥为 y ，私钥为 x

• 签名

  对于消息 m ，首先随机选取整数 k ，$ 1 \leq k \leq p-2 $,然后计算

  $$ r = g^k \bmod p, s = (h(m) -x \cdot r) \cdot k^{-1} \bmod (p-1) $$

  则 m 的签名为 $(r,s)$,其中 h 为 Hash函数

• 验证

  接收方在收到消息 m 和 签名 $(r,s)$ 后，验证

  $$ y^r \cdot r^s = g^{h(m)} \bmod p$$

  如果等式成立 ，则 $(r,s)$ 是消息 m 的有效签名，反之无效

• 正确性

  • 因为 $ s = (h(m) - x \cdot r) \cdot k^{-1} \bmod (p-1)$

  • 所以 $ s \cdot k + x \cdot r = h(m) \bmod (p-1)$

  • 所以 $ g^{h(m)} = g^{(s \cdot k + x \cdot r)} = g^{sk} \cdot g^{xr} = y^r \cdot r^s \bmod p$

  • note: $y = g^x \bmod p$ , $r = g^k \bmod p$

    ​ 如果消息 m 被篡改，则 h(m) 发生改变，从而 $y^r \cdot r^s \neq g^{h(m)} $ 起到验证作用

讨论两问题

（1） 用EIGamal方案计算一个签名时，使用的随机数 K 能不能被泄露

（2） 若Bob使用相同的 K 的值来签名不同的两份消息， Oscar能否攻破这个体制

Answer1:

• 由于私钥 x 是保密的，所以如果攻击者想要得到这个密钥，必须求解离散对数问题 $\log_gy$ ,这是一个困难问题。但是随机数 K 泄露，则可解 $ x = (h(m) - sk)r^{-1} \bmod (p-1)$ 得到 x，方案被攻破
• note：为什么 K 泄露方案会被攻破呢
  • 先看看公开参数有什么
    • 大素数 P
    • 生成元 g
    • 公钥 y ，y 由 $ y= g^x \bmod p$ 得到
    • 签名一 r ，r 由 $r=g^k \bmod p$ 得到
    • 签名二 s , s 由 $s = (h(m) -x \cdot r) \cdot k^{-1} \bmod (p-1)$ 得到
  • 现在假设我们是中间人，我们可以获得这些消息，并想篡改消息 m，但是一旦篡改消息 m，会导致 h(m) 发生改变，从而导致 $$y^r \cdot r^s \neq g^{h(m)} $$ ，接收者就知道消息已被篡改。因此想要不被发现，必须连带着把 r ,s 也一起改变，即重新计算 $$s = (h(m) -x \cdot r) \cdot k^{-1} \bmod (p-1) $$ ，得到 $s’$ ,并发送篡改后的签名 $(r,s’)$，这样接收方就无法判断消息是否被篡改
  • 所以现在的问题是，如何计算 $s’$ ? 看看 s 的生成式，我们必须知道 x 和 k 才能计算 s
  • 我们手上现在跟 K 相关的式子只有两条 $r=g^k \bmod p$ 和 $s = (h(m) -x \cdot r) \cdot k^{-1} \bmod (p-1)$ ，显然我们应该用前面那一条式子，因为后面的式子有两个未知数
  • 那就来看看第一个式子吧， 我们现在知道 $r, g, p$，需要求 g 的几次方模 p 等于 r ，然而这是个很困难的问题，也就是离散对数问题，EIGamal的安全性就基于此。
  • 一旦 K 泄露，就可以计算出 x ，整个消息就可以被篡改并进行重新签名得到 $s’$

Answer2:

• 不可用同一个 K 做两次签名。若Bob利用相同 K 签名两次，即签名分别为 $(r,s_1)$ ,$(r,s_2)$ ,则Oscar可以联立方程

  $$
  \begin{cases}
  h(m1) = xr +ks_1 \bmod (p-1) \newline h(m2) = xr +ks_2 \bmod (p-1)
  \end{cases}
  $$

  可得： $ x = [h(m_1)s_2 - h(m_2)s_1] (s_2 - s_1) ^{-1} r^{-1} \bmod (p-1) $

• note： 上式乘 $s_2$, 下式乘 $s_1$ 即可

​

DSS签名算法

数字签名标准DSS(Digital Signature Standard)是由美国NIST公布的联邦信息处理标准FIPS PUB 186，最初于1991年公布，在考虑了公众归队其安全性的反馈意见后，于1993年公布了其修改版

• DSS的基本方式

  首先将DSS与RSA的签名方式做一比较。RSA算法既能用于加密和签名，又能用于密钥交换。与此不同，DSS使用的算法只能提供数字签名功能。下图是比较

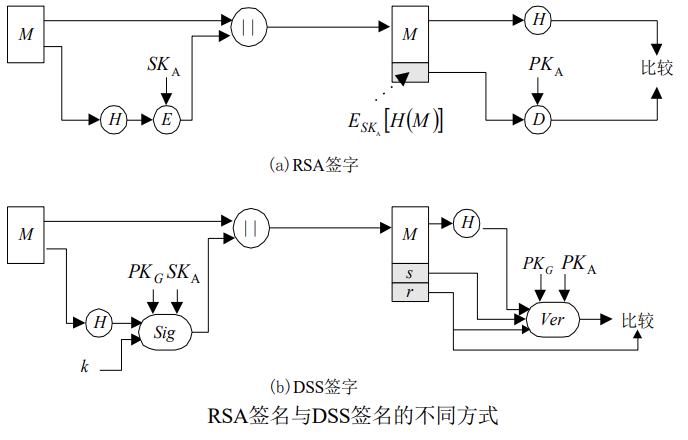
密钥生成

• 设 $512 \leq L \leq 1024$ 且 $L$ 是64的倍数，选取 $2^{L-1} < p <2^L$ 大素数，其满足存在160比特的素数$q|p-1$

• 随机选取整数 $h$ ,$ 1 < h <p-1 $ ,且使 $ g = h^{(p-1) /q} \bmod p $ , $p,g$ 公开

• 随机选取整数 $x$ , $1 \leq x \leq q-1 $ , 计算 $ y = g^x \bmod p $

• 公钥为 $y$, 私钥为 $x$

签名

• 对于消息 m ，首先随机选取一个整数 k，$1 \leq k \leq p-2 $ ,然后计算
  $$ {left}
  \begin{align}
  &r = (g^k \bmod p ) \bmod q \
  &s = (h(m) + xr) K^{-1} \bmod q
  \end{align}
  $$
  则 m 的签名为 $(r,s$) ,其中 h 为Hash函数SHA

验证

• 接收方收到消息 m 和 签名 $(r,s$)，后计算
  $$
  \begin{align}
  u_1 &= h(m) s^{-1} \bmod q \newline
  u_2 &= rs^{-1} \bmod q
  \end{align}
  $$

• 验证等式
  $$
  (g^{u_1}y^{u_2} \bmod p) \bmod q =r
  $$

• 如果等式成立，则$(r,s)$ 消息 m 的有效签名

正确性

• 因为 $u_1 + xu_2 \bmod q = (h(m) + xr)s^{-1} \bmod q = k$

• 所以
  $$
  \begin{align}
  g^{u_1}y^{u_2} \bmod p \bmod q &= g^{u_1+ xu_2} \bmod p \bmod q \newline
  &= g^k \bmod p \bmod q \newline
  &=r
  \end{align}
  $$

特殊性质的签名算法

盲签名

概念

• 盲签名方案是在发送者 A 和发送者 B 之间的双方协议。其基本思想如下：
  • A 发送给 B 一段消息，B 对它签名并送回 A
  • 从这个签名 A 能够计算 B 关于 A 预先所选消息 m 的签名
  • 协议完成时 B 既不知道消息 m 也不知道消息的签名
• 盲签名的目的是防止 B 看到消息和签名，从而使 B 以后不能将所签消息和发送者 A 联系起来

应用

• 发送者 A（客户）不希望签名者 B（银行）能够将一条先验消息 m 及其签名 $S_B(m)$ 与协议的特定实例相联系
• 这个特性在电子现金应用中可能很重要，因为那里的消息也许表示 A 所花的金钱数额
• 当 m 和 $S_B(m)$ 提交给 B 进行支付时， B 无法推断原先接收签名的是谁。这就是允许 A 的匿名性，从而 A 的消费模式不能被监测

所需组件

• 签名者 B 的一种数字签名机制，用 $S_B(x)$ 记 B 对 x 签名
• 函数 $f$ 和 $g$ （只有发送者知道），满足$g(S_B(f(m))) = S_B(m)$ 。其中 $f$ 叫盲化函数，$g$ 叫去盲函数，$f(m)$ 叫做盲消息。此条对 $S_B$ 和 $g$ 的选择加了许多限制

Chaum 盲签名协议

• 摘要：发送者 A 接收 B 关于盲消息的签名。由此 A 计算 B 关于 A 预先所选消息 m 的签名，$0 \leq m \leq n-1 $ 。B 既没有消息 m 也没有 m 相关签名的知识
  • B 的RSA公钥和私钥分别是 $(n,e)$ 和 $d$ 。k 是 A 随机选择秘密数，满足 $ 0 \leq k \leq n-1$ 且 $gcd(n,k) =1 $
  • 协议步骤
    • （盲化） A 计算 $m^* = mk^e \bmod n$
    • （签名） B 计算 $s^* = (m^*) ^d \bmod n $
    • （去盲） A 计算 $s=k^{-1} s^* \bmod n$
• 正确性
  • 显然 s 是 m 的签名 ，即 $s=m^d \bmod n$
  • B 既没有消息 m 也没有 m 相关签名 s 的知识

不可追踪电子现金

• Chaum, Fiat, 和Naor提出一个不可追踪电子现金方案。

  • 加入者A获取来自银行的电子现金货币 – A可以将此货币在商店B花掉，而B无需与银行在线验证货币的真实性。 – 当B在银行将电子货币兑现时，银行不能将其与A联系起来。
  • 如果A企图以该货币花两次（重复消费），那么A的身份就会暴露。

• Okamoto提出一种可分电子现金方案。可分电子硬币是一个 与金钱数值关联的元素，可用来进行多次电子买卖，前提是 所有交易的金钱总额不超过硬币数额

不可否认签名

概念

• 不可否认的数字签名由 CHaum 和 van Antwerpen 在1989年提出
• 不可否认签名没有签名者的合作，接收者无法验证签名

应用

• 实体 A（客户）希望访问被实体 B（银行）控制的某个安全区域。比如该安全区域可能是存放保险箱的房间。在许可访问之前，B 要求 A 签署一份时间和日期的文件。如果 A 采用了不可否认签名，那么在验证过程中没有 A 的直接参与， （在以后的日期）B 就不能向任何人证明 A 使用过安全区域中的设施
• 假定某大公司 A 制作了一个软件包。A 对软件包签名并将它卖给实体 B，而 B 决定将其拷贝再卖给第三方C，那么没有 A 的合作 C 就无法验证该软件是否正版
  • 当然，这种措施并 不能阻止 B 用它自己的签名重新签署软件包，但因此 B 也就 无法利用 与 A 名气相关的市场利益。而且 追踪 B 的欺诈行为也将很 容易

组成

• 一个不可否认签名方案有三部分组成：
• 签名算法
• 验证协议
• 否认协议

其他

• 签名者可以声称一个签名是伪造的，在这种情况下，如果 签名者拒绝 参加验证，就可认为签名者有欺骗行为。如果签名者 参加 验证，由否认协议就可推断出签名的 真伪 。
• 否认协议需要做到以下两点
• B能使A相信一个不合法的签名是伪造的。
• B以很小的概率使A相信一个合法签名是伪造的
• 不可否认签名的一个 不足之处 是签名者有可能不在场或者拒绝合作，而导致签名无法被接收者验证。
  • Chaum提出“指定验证者签名”的概念，其中签名者指定某 实体作为签名的验证者。
  • 一旦签名者不在场或者拒绝合作，验证者就有权力与接收 者交互来检查签名。
  • 验证者不能产生签名者的签名

群签名

概念

• 1991年，Chaum和Van Heijst提出群签名方案。
• 该方案允许群众的某个成员以群的名义匿名地签发消息。满足下述三个条件：
  • 只有 群中的成员才能代表群进行签名；
  • 签名的接收者 能验证 签名是哪一个群的一个合法签名，但 不能分辨 具体的签名者。
  • 一旦出现争端，可借助群成员或一个可信的机构能 识别出签名者

应用

• 一个公司有几台计算机，每台都联在局域网上。公司的 每个部门 有其自己的打印机（也连在局域网上），并且 只有本部门 的人员才能允许使用其部门的打印机。因此，打印前必须 确认 用户在哪个部门工作。同时公司为了保密，不可以暴露用户的身份。然而，如果有人 滥用 打印机，主管者必须能 找出 是谁在滥用打印机

组成

（1）建立（setup） 一个用以产生群公钥和私钥的多项式概率算法。

（2）加入（join） 一个用户和群管理员之间的交互式协议。执行该协议可以使用户成为群成员，群管理员得到群成员的秘密的成员管理密钥，并产生群成员的私钥和成员证书。

（3）签名（sign） 一个概率算法，当输入一个消息、一个群成员 的私钥和一个群公钥后，输出对该消息的签名。

（4）验证（verify） 给定一个消息的签名和一个群公钥后，判断该签名相对于该群公钥是否有效。

（5）打开（open） 给定一个签名、群公钥和群私钥的条件下确定 签名者的身份

性质

① 正确性（correctness）

② 不可伪造性（unforgeability）

③ 匿名性（anonymity）

④ 不可关联性（unlinkability）

⑤ 可跟踪性（traceability）

⑥ 可开脱性（exculpability）

⑦ 抗联合攻击（coalition-resistance）

代理签名

<TODO：概念> (他PPT也妹给啊)

组成

• 系统建立 选定代理签名方案的系统参数，用户的密钥等
• 签名权力的委托 原始签名者将自己的签名权力委托给代理签名 者
• 代理签名的产生 代理签名者代表原始签名者产生代理签名
• 代理签名的验证 验证人验证代理签名的有效性。

分类

根据签名权力委托的方式不同，代理签名可以分为以下几类：

（1）完全代理（full delegation）

（2）部分代理（partial delegation）

（3）具有证书的代理（delegation by warrant）

（4）具有证书的部分代理（partial delegation with warrant）

根据原始签名者能否产生同代理签名者一样的签名，代理签名又 可分为两类：

（1）代理非保护（proxy-unprotected） 原始签名者能够产生有效的 代理签名。

（2）代理保护（proxy-protected） 原始签名者不能够产生有效的代 理签名

强代理方案满足性质：

① 可区分性（distinguishability）

② 可验证性（verifiability）

③ 强不可伪造性（strong unforgeability）

④ 强可识别性（strong identifiability）

⑤ 强不可否认性（strong undeniability） ⑥ 防止滥用（prevention of misuse）